En el vasto mundo de las matemáticas, el concepto de recíproco juega un papel fundamental en diversas áreas, desde la aritmética básica hasta el álgebra avanzada. Comprender cómo se determina el recíproco de un número no solo es esencial para resolver problemas matemáticos, sino que también tiene aplicaciones en la vida cotidiana, desde la cocina hasta las finanzas. Este artículo se adentrará en lo que significa el recíproco de un número, cómo se calcula y proporcionará ejemplos prácticos para facilitar la comprensión del tema.
Además, exploraremos la relación entre el recíproco y otros conceptos matemáticos, así como su importancia en el contexto de las fracciones y las divisiones. Al finalizar, los lectores tendrán una comprensión sólida de "el recíproco de un número ejemplos" que les permitirá aplicar este conocimiento en diversas situaciones. Así que, ¡comencemos a desentrañar este fascinante tema!
¿Qué es exactamente un recíproco? ¿Cómo se puede calcular para cualquier número? A lo largo de este artículo, responderemos a estas preguntas y más, asegurándonos de que la comprensión del recíproco sea clara y accesible para todos. Los ejemplos proporcionados ilustrarán no solo cómo se determina el recíproco, sino también cómo se utiliza en diferentes contextos matemáticos.
¿Qué es el recíproco de un número?
El recíproco de un número es simplemente uno dividido por ese número. Matemáticamente, si tenemos un número 'x', su recíproco se expresa como 1/x. Por ejemplo, si 'x' es 2, el recíproco sería 1/2. Este concepto es fundamental en las matemáticas, ya que permite realizar divisiones y facilitar operaciones con fracciones.
¿Cómo se calcula el recíproco de un número?
Calcular el recíproco de un número es un proceso sencillo. Aquí hay un paso a paso:
- Identifica el número del cual deseas encontrar el recíproco.
- Realiza la operación de división: 1 dividido por ese número.
Por ejemplo, para calcular el recíproco de 4, simplemente haces 1/4, lo que resulta en 0.25.
Ejemplos prácticos de recíprocos
A continuación, se presentan algunos ejemplos de cómo se calcula el recíproco de diferentes números:
- Recíproco de 5: 1/5 = 0.2
- Recíproco de 10: 1/10 = 0.1
- Recíproco de -3: 1/(-3) = -0.3333
Estos ejemplos demuestran que los recíprocos pueden ser tanto positivos como negativos, dependiendo del número original.
¿Por qué es importante entender el recíproco?
Comprender el recíproco es fundamental por varias razones. Primero, permite simplificar operaciones matemáticas complejas. En segundo lugar, es crucial para resolver ecuaciones algebraicas donde se requiere invertir fracciones. Además, el recíproco es esencial en la teoría de números y en la comprensión de proporciones y porcentajes.
¿Cómo se relaciona el recíproco con fracciones?
El recíproco está estrechamente relacionado con las fracciones. Cuando multiplicas un número por su recíproco, el resultado siempre es 1. Esto se puede expresar de la siguiente manera:
Si 'a' es un número y 'b' es su recíproco, entonces:
a * b = 1
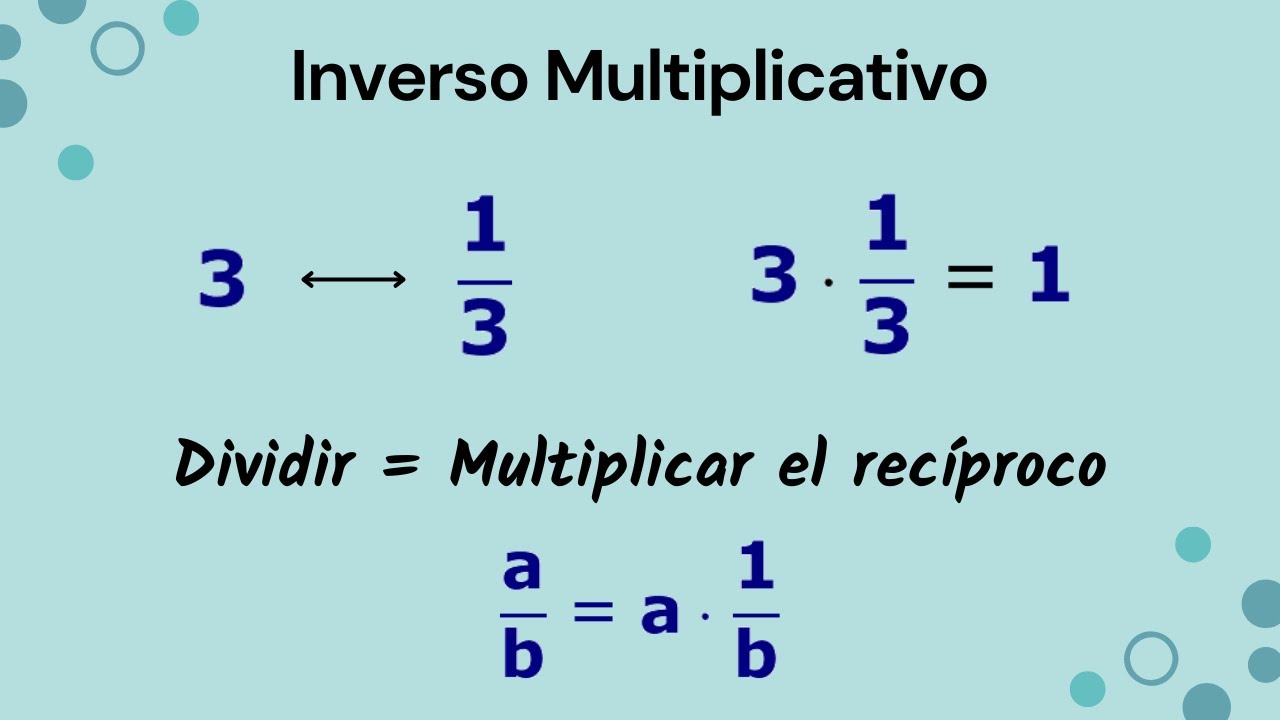
Por ejemplo, si tomas 3 y su recíproco 1/3, al multiplicarlos obtendrás:
3 * (1/3) = 1
Ejemplos de recíprocos en fracciones
Aquí hay algunos ejemplos de cómo funciona el recíproco en fracciones:
- Recíproco de 1/2: 2/1 = 2
- Recíproco de 3/4: 4/3
- Recíproco de 5/6: 6/5
Estos ejemplos muestran cómo el recíproco de una fracción es simplemente la inversión de la fracción original.
¿Cuáles son las aplicaciones prácticas del recíproco?
El recíproco tiene muchas aplicaciones prácticas en la vida cotidiana. Desde la cocina, donde las recetas pueden requerir conversiones de medidas, hasta las finanzas, donde se necesita calcular tasas de interés o dividir costos. Aquí hay algunas situaciones comunes donde el recíproco es útil:
- Calcular proporciones en recetas de cocina.
- Determinar tasas de retorno en inversiones financieras.
- Resolver problemas de velocidad y tiempo.
¿Cómo se enseña el recíproco en las aulas?
La enseñanza del recíproco en el aula suele incluir ejemplos visuales y prácticos para ayudar a los estudiantes a comprender el concepto. Los maestros pueden utilizar diagramas, juegos de matemáticas y ejercicios prácticos para demostrar cómo se calcula y se aplica el recíproco en diferentes contextos.
Conclusión: Comprendiendo "el recíproco de un número ejemplos"
En resumen, el recíproco de un número es un concepto clave en el mundo de las matemáticas, y entender cómo se calcula y aplica es vital para resolver problemas en diversas áreas. A través de ejemplos y explicaciones claras, hemos explorado el significado de "el recíproco de un número ejemplos", así como su importancia en la vida cotidiana. Ya sea que estés en el aula, en la cocina o manejando tus finanzas, el recíproco tendrá un lugar en tu vida matemática.
Article Recommendations
- How Old Is Brielle From Ellen
- Robert James Ritchie Jr
- Evangeline Lilly Parents
- Glenn Close Michael Douglas
- How Old Is Helena Vestergaard
- Black Donals Trump
- How Many Female Governors
- Nigerian Actors Hollywood
- Jenna Ushkowitz
- Good Morning Quote For A Friend
