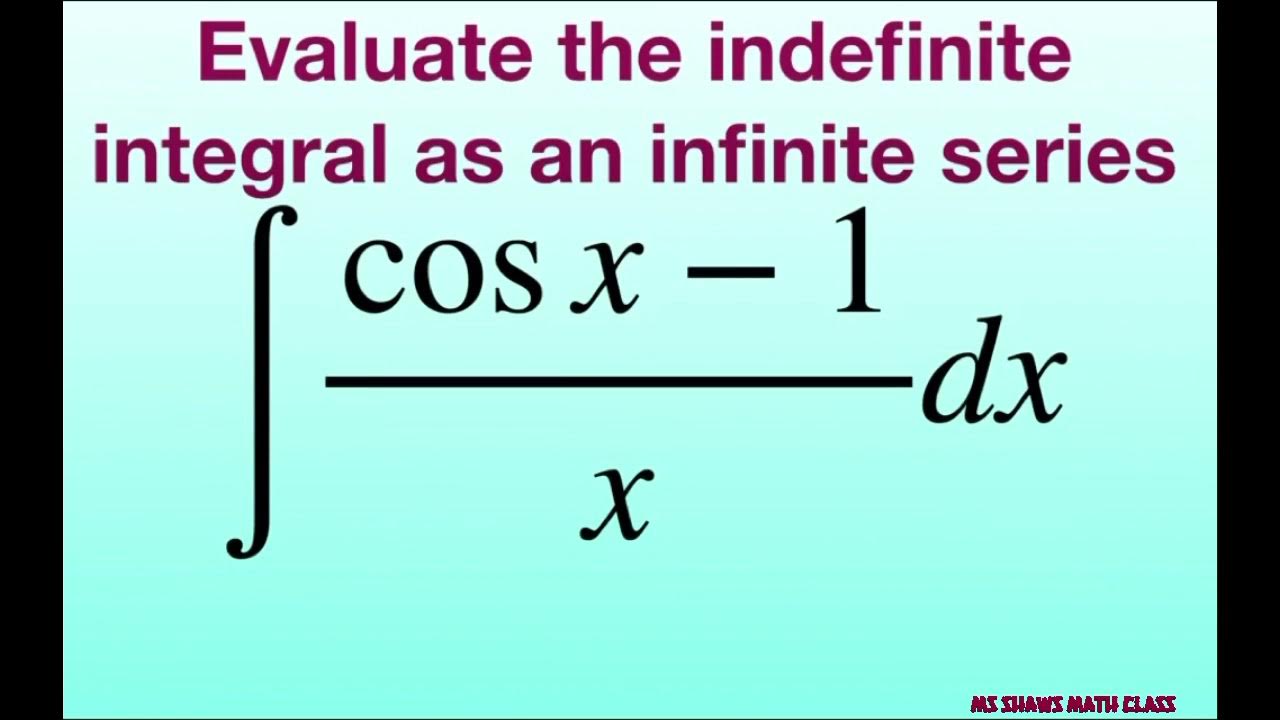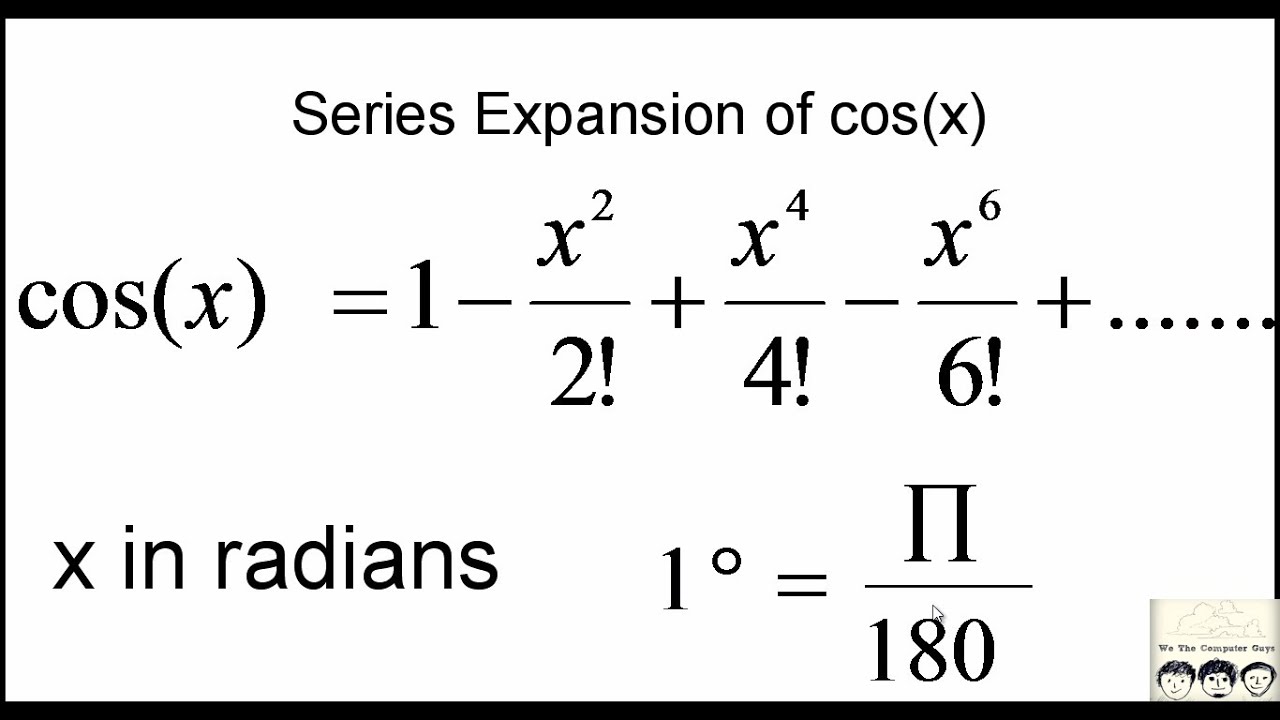The study of power series is an essential part of mathematical analysis, particularly when it comes to approximating functions. Among the various functions we encounter, the cosine function stands out due to its periodic nature and its applications in various fields such as physics, engineering, and computer science. Understanding the power series expansion of cos x allows us to evaluate the function at points where it may be challenging to compute directly. Moreover, this expansion reveals intricate relationships between calculus and trigonometry, showcasing the beauty of mathematical concepts.
In this article, we will dive into the details of the power series for cos x, exploring its derivation, properties, and practical applications. We will also address common questions and misconceptions surrounding the topic. Whether you are a student looking to grasp the foundations of power series or a professional seeking to enhance your mathematical toolkit, this comprehensive guide is designed for you.
Join us as we uncover the world of power series cos x, and discover how this mathematical tool can simplify complex problems and enhance our understanding of trigonometric functions. Prepare to embark on a journey through power series, with cos x as our guide, illuminating the path to deeper mathematical insights.
What is a Power Series?
A power series is an infinite series of the form:
S(x) = a0 + a1x + a2x² + a3x³ + ... + anx^n
where the coefficients a0, a1, a2, etc., are constants, and x is a variable. This representation allows functions to be expressed as an infinite sum of terms, making it easier to analyze and manipulate them.
How is the Power Series for Cos x Derived?
The power series for cos x can be derived using Taylor series expansion. The Taylor series of a function f(x) around a point a is given by:
f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)²/2! + ...
For cos x, we can evaluate the derivatives at a = 0:
- cos(0) = 1
- cos'(0) = 0
- cos''(0) = -1
- cos'''(0) = 0
- cos''''(0) = 1
As we can see, the derivatives yield a repeating pattern. Thus, the power series for cos x centered at 0 is:
cos x = 1 - (x²/2!) + (x⁴/4!) - (x⁶/6!) + ...
What are the Key Properties of the Power Series for Cos x?
- The series converges for all values of x (entire function).
- It is an even function, meaning cos(-x) = cos(x).
- The coefficients alternate in sign, reflecting the oscillating nature of the cosine function.
- The series can be truncated for approximations, yielding good estimates for small values of x.
What is the Radius of Convergence for the Power Series of Cos x?
The radius of convergence for a power series can be determined using the ratio test. For the power series of cos x, since the factorial in the denominator grows faster than the polynomial in the numerator, the series converges for all x. Therefore, the radius of convergence is:
R = ∞
How is the Power Series for Cos x Used in Real-Life Applications?
The power series for cos x has numerous practical applications across various fields:
- Physics: Used in wave mechanics and oscillatory motion analysis.
- Engineering: Applied in signal processing and control systems.
- Computer Science: Utilized in algorithms for calculating trigonometric functions.
- Finance: Used in modeling periodic trends in financial data.
Can the Power Series for Cos x Help with Calculating Trigonometric Values?
Yes, the power series for cos x allows for the computation of cosine values at points where a calculator might not be handy. By truncating the series after a few terms, we can obtain a reasonably accurate estimate of cos x.
For example, to approximate cos(0.1), we can use:
cos(0.1) ≈ 1 - (0.1²/2!) + (0.1⁴/4!)
Calculating the terms:
cos(0.1) ≈ 1 - 0.005 + 0.00041667 ≈ 0.995
How Can We Visualize the Power Series for Cos x?
Visualizing the power series for cos x can enhance our understanding of how the series converges to the actual cosine function. By plotting the first few terms of the series alongside the cosine function, we can observe how the approximation improves as more terms are added. This can be done using graphing software or programming languages such as Python or MATLAB.
Conclusion: The Significance of Power Series in Mathematics
In conclusion, the power series for cos x is a powerful mathematical tool that helps us approximate the function and understand its properties. The derivation and application of this series demonstrate the interconnectedness of calculus, trigonometry, and real-world problems. As we continue to explore the vast landscape of mathematics, the power series cos x will remain a fundamental concept that underpins many advanced topics and applications.
Article Recommendations
- De Donde Es La Mama De Donal Trump
- Birthday January 16 Astrologyl
- Finalists On Dancing With The Stars
- How Old Is Brielle From Ellen
- Jenna Ushkowitz
- Anime Character Male
- Aj And Kandi Burruss
- What Happened To Adam Cartwright
- Percy Jackson Logan Lerman
- Black Donals Trump