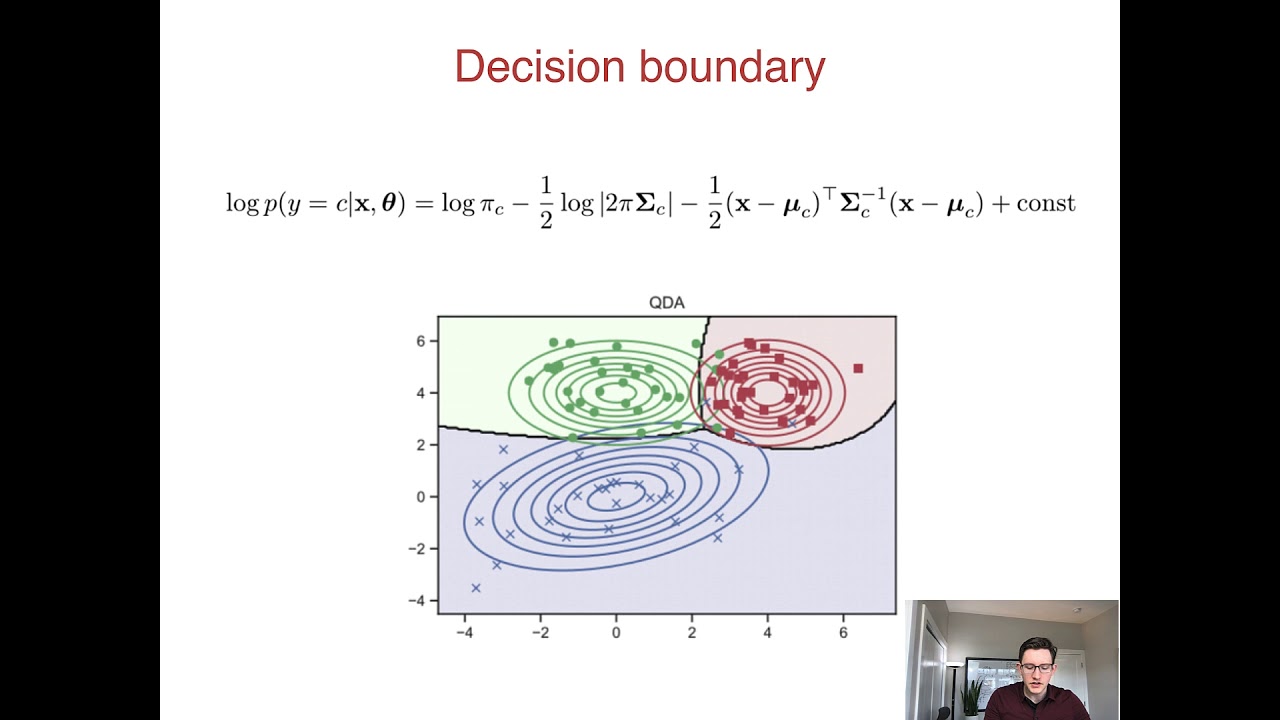
In the realm of machine learning and statistics, Gaussian Discriminant Analysis (GDA) stands out as a powerful classification technique that leverages the principles of probability theory. This methodology is particularly celebrated for its ability to establish a clear decision boundary between different classes by modeling the distribution of the data points. By assuming that the data follows a Gaussian distribution, GDA simplifies complex problems, making it an essential tool for data scientists and analysts alike.
Understanding Gaussian Discriminant Analysis requires delving into its foundational concepts and applications. The method hinges on the idea of maximizing the likelihood of classifying data points correctly based on their features. This probabilistic approach not only enhances classification accuracy but also facilitates insights into the underlying structure of the data. As organizations increasingly rely on data-driven decisions, GDA emerges as a crucial technique in the arsenal of modern analytics.
As we explore the intricacies of Gaussian Discriminant Analysis, we'll uncover its practical implications, advantages, and limitations, and address common questions that arise when implementing this technique. The following sections will guide you through the essential aspects of GDA, equipping you with the knowledge needed to apply it effectively in various scenarios.
What is Gaussian Discriminant Analysis?
Gaussian Discriminant Analysis is a statistical method used for classification tasks. At its core, it aims to distinguish between two or more classes by modeling the distribution of features within each class using Gaussian distributions. This allows for the computation of a decision boundary that optimally separates the classes based on their probability distributions.
How Does Gaussian Discriminant Analysis Work?
The workings of Gaussian Discriminant Analysis can be summarized in a few key steps:
- Data Preparation: Collect and preprocess the data, ensuring it is clean and formatted correctly.
- Feature Analysis: Identify relevant features that contribute to class separation.
- Modeling Distributions: Fit Gaussian distributions to the features of each class.
- Decision Boundary: Compute the decision boundary based on the likelihood of belonging to each class.
What Are the Assumptions of Gaussian Discriminant Analysis?
Gaussian Discriminant Analysis operates under several key assumptions:
- Normal Distribution: Each class's features are assumed to follow a Gaussian distribution.
- Equal Covariance: It's assumed that all classes share the same covariance matrix, which simplifies the decision boundary computation.
- Independence: Features are assumed to be independent of one another, which may not always hold true in real-world scenarios.
What Are the Advantages of Using Gaussian Discriminant Analysis?
Gaussian Discriminant Analysis offers several advantages for classification tasks:
- Interpretability: The probabilistic nature of GDA provides insights into the classification process.
- Efficiency: GDA can be computationally efficient, especially with smaller datasets.
- Robustness: It performs well when the assumptions of normality and equal covariance are reasonably satisfied.
Are There Any Limitations to Gaussian Discriminant Analysis?
Despite its strengths, Gaussian Discriminant Analysis has notable limitations:
- Assumption Sensitivity: The accuracy of GDA heavily relies on the validity of its assumptions.
- Non-linear Boundaries: GDA may struggle with datasets exhibiting non-linear class boundaries.
- Outlier Sensitivity: The presence of outliers can significantly skew the results.
How to Implement Gaussian Discriminant Analysis in Python?
Implementing Gaussian Discriminant Analysis in Python is straightforward, especially with libraries like Scikit-learn. Below is a basic outline of the steps involved:
- Import necessary libraries:
- Load the dataset and split it into training and testing sets.
- Initialize the GDA model and fit it to the training data.
- Make predictions on the testing set and evaluate the model's performance.
What Are the Real-World Applications of Gaussian Discriminant Analysis?
Gaussian Discriminant Analysis finds applications across various domains, including:
- Medical Diagnosis: Classifying patients based on symptoms and diagnostic features.
- Image Recognition: Identifying objects in images by analyzing pixel distributions.
- Finance: Credit scoring and risk assessment based on customer data.
Conclusion: Why Choose Gaussian Discriminant Analysis?
Choosing Gaussian Discriminant Analysis for classification tasks can yield significant benefits, particularly when dealing with data that aligns with its assumptions. By understanding the fundamentals of GDA, its advantages, limitations, and real-world applications, data scientists and analysts can make informed decisions on when and how to leverage this powerful technique. Whether you're working in healthcare, finance, or any data-driven field, Gaussian Discriminant Analysis is a valuable tool that can enhance your analytical capabilities.
Article Recommendations
- Stevie Nicks Bio
- Rod Steart Age
- Who Plays Ally In Austin And Ally
- Glenn Close Michael Douglas
- Primetime Emmy Award For Outstanding Reality Program
- Finalists On Dancing With The Stars
- Which Shark Vacuum Is Better
- The Prince Of Denmark
- How Many Female Governors
- John Krasinski Weight
