Mathematics is a realm filled with intriguing concepts and numbers that often lead to endless curiosity. Among these concepts, the cube root stands out as a pivotal operation, especially when applied to unique numbers like 11. Understanding the cube root of a number not only enhances our numerical prowess but also opens doors to deeper mathematical explorations. The cube root of 11, while it may seem like a simple computation, is a gateway to understanding more complex theories and applications in mathematics.
The cube root of a number is defined as a value that, when multiplied by itself twice, gives the original number. In the case of 11, the cube root is represented mathematically as ∛11. This value is not a whole number, and its decimal expansion is non-repeating and non-terminating, making it an intriguing figure for both students and math enthusiasts alike. As we delve deeper into the cube root of 11, we will uncover its significance in various mathematical contexts and its applications in real-world scenarios.
In this article, we will explore the cube root of 11 from multiple angles, including its calculation, significance, and applications in different fields. Whether you are a student looking to understand the concept better or simply someone with a passion for numbers, this exploration of the cube root of 11 is sure to pique your interest.
What is the Cube Root of 11?
The cube root of 11, denoted as ∛11, is the number that, when multiplied by itself three times, results in 11. To find the cube root of 11, we can use various methods, including estimation and calculator functions. The approximate value of the cube root of 11 is about 2.224. This means that 2.224 × 2.224 × 2.224 ≈ 11. Understanding this value can help in various applications, including scientific calculations and mathematical modeling.
How Can We Calculate the Cube Root of 11?
Calculating the cube root of 11 can be done through several methods:
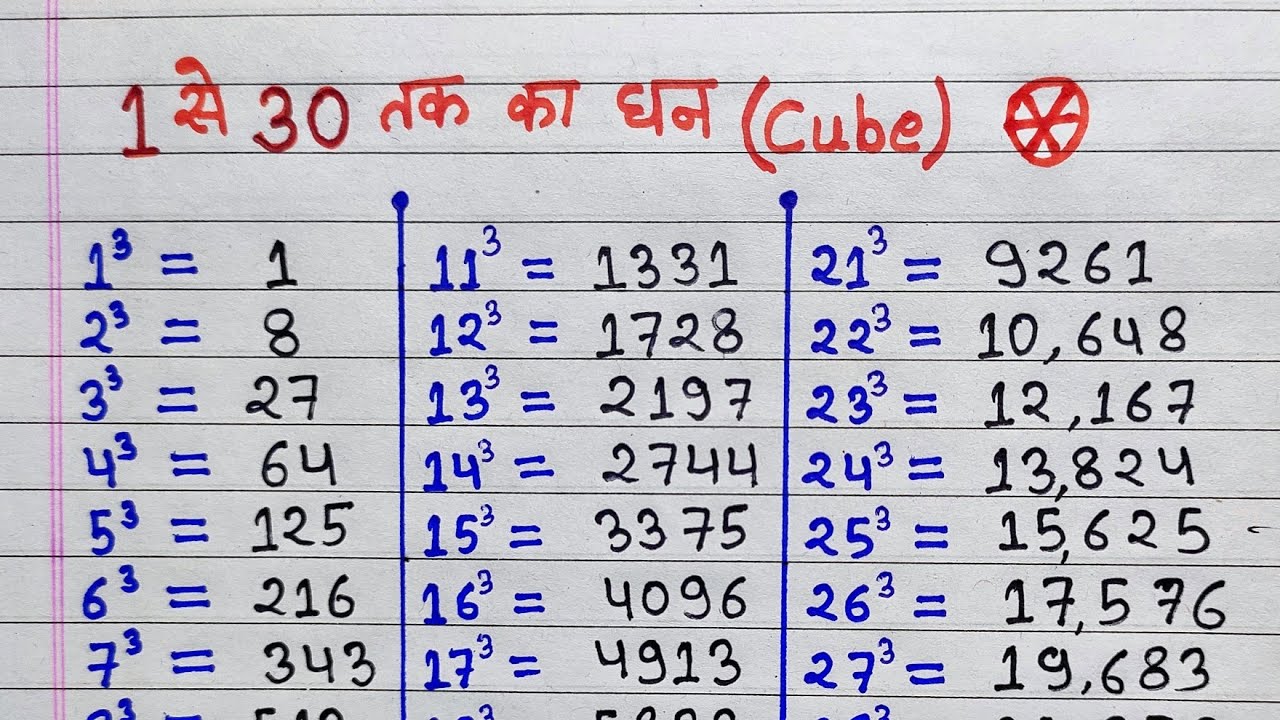
- Estimation: Since 2^3 = 8 and 3^3 = 27, we know that the cube root of 11 lies between 2 and 3. We can refine our estimate further by testing values between 2 and 3.
- Using a Calculator: Most scientific calculators have a cube root function that allows for quick calculations.
- Using Mathematical Formulas: For those inclined towards algebra, the formula √(x) = x^(1/3) can also be employed to find cube roots.
Why is the Cube Root of 11 Important?
The cube root of 11 is significant in various mathematical fields. It can be used in:
- Geometry: Understanding the dimensions of cubes and their volumes.
- Physics: Analyzing properties of materials and phenomena that involve cubic relationships.
- Engineering: Designing structures and systems that rely on cubic measurements.
What Applications Does the Cube Root of 11 Have?
The applications of the cube root of 11 extend beyond mere calculations. Here are a few notable applications:
1. Architecture and Construction
In architecture, the cube root of 11 can help in determining the volume of spaces or materials needed for construction. For example, if a cubic container needs to hold a specific volume of 11 cubic units, knowing the cube root assists builders in figuring out the dimensions of the container.
2. Scientific Research
In scientific research, cubic relationships often arise in fields such as chemistry and physics. Understanding the cube root of 11 can provide insights into molecular structures and reactions where cubic arrangements are relevant.
3. Computer Graphics
In computer graphics, the cube root of 11 can assist in rendering three-dimensional objects accurately. It is vital for programmers to understand volumetric calculations when creating realistic models.
Can We Visualize the Cube Root of 11?
Visualizing the cube root of 11 involves understanding its placement within the number line and its relationship with nearby cubes:
- The cube of 2 is 8, and the cube of 3 is 27.
- Thus, ∛11 is between 2 and 3, making it easier to visualize its location.
How Does the Cube Root of 11 Compare to Other Numbers?
The cube root of 11 can be compared with the cube roots of other integers to draw interesting conclusions:
1. Comparison with Perfect Cubes
Perfect cubes like 1 (1^3), 8 (2^3), and 27 (3^3) provide a reference point for understanding the cube root of 11. Unlike perfect cubes, the cube root of 11 is an irrational number, which adds to its uniqueness.
2. Estimation Techniques
When estimating cube roots, knowing that ∛11 lies between 2.2 and 2.3 can help in various mathematical problems. This range allows students to understand how to approach cube root calculations.
What Are the Limitations of the Cube Root of 11?
While the cube root of 11 is useful, it also has limitations:
- It is an irrational number, meaning it cannot be expressed as a simple fraction.
- Approximation methods can introduce errors, especially in precise calculations.
Conclusion: Embracing the Cube Root of 11
In summary, the cube root of 11 is more than just a number; it represents a fascinating concept that intertwines with various aspects of mathematics, science, and engineering. By understanding the cube root of 11, we not only enhance our mathematical skills but also gain insights into its practical applications in everyday life. As we continue to explore the world of numbers, let the cube root of 11 inspire curiosity and a love for learning.
Article Recommendations
- The Prince Of Denmark
- What Team Does Anthony Rizzo Play For
- Cuanto Tiempo Gobernara Donal Trump
- Liza Weil
- What Former Presidents Are Still Alive
- Birthday January 16 Astrologyl
- Ideas For Duo Day
- Who Plays Ally In Austin And Ally
- Reggie Mathis
- Robert James Ritchie Jr
